这是一篇不可多得的好文章，将无监督的深度生成模型与变分贝叶斯模型结合在一起。它包含两部分，一部分是probabilistic encoder $Q_{\Phi}(Z|X)$，用来近似真实的后验分布$P_{\Theta}(Z|X)$，将输入$X$映射到隐含层编码$Z$；另一部分是生成模型$P_{\Theta}(X|Z)$【decoder】，用隐含层的表示重构输入$X$

---

在机器学习里，我们常常要求解像$P_{\Theta}(X)=\int P_{\Theta}(X|Z)P_{\Theta}(Z)dZ$这样的似然模型，其中$Z$是隐变量。为了求解这样的模型，如果$Z$的后验分布$P(Z|X,\Theta)$是tractable的，那么我们可以用EM算法来求解；否则，一种常用的方法就是用变分贝叶斯【VB】，用形式简单的分布$Q(Z)$去近似$P(Z|X,\Theta)$。
在VB里，我们是将似然函数分解成一个lower bound加上近似分布与真实后验分布的KL距离，即：
\begin{align}
lnP_{\Theta}(X) &= E_{Q_{\Phi}(Z|X)}[-lnQ_{\Phi}(Z|X)+lnP_{\Theta}(X,Z)] + D_{KL}(Q_{\Phi}(Z|X)||P_{\Theta}(Z|X)) \\
&\ge E_{Q_{\Phi}(Z|X)}[-lnQ_{\Phi}(Z|X)+lnP_{\Theta}(X,Z)] \\
&= -D_{KL}(Q_{\Phi}(Z|X)||P_{\Theta}(Z)) + E_{Q_{\Phi}(Z|X)}[lnP_{\Theta}(X|Z)] \\
&= \mathcal{L}(X;\Theta, \Phi)
\end{align}
在VAE里，我们通过优化这个下界，求解我们的极大似然模型，所以这也就是网络的loss函数。其中，第一项就是约束后验分布与先验分布之间的距离；第二项其实就是给定隐含层表示，重构出$X$的期望，所以这一项可以用传统Autoencoder里的重构误差来代替。
然而，直接蒙特卡洛【minibatch】做梯度估计的variance会比较大，所以作者提出了一个reparameterization trick: 将随机变量$\tilde{z} \sim Q_{\Phi}(Z|X)$用一个可导的确定性转换$g_{\phi}(\epsilon,X)$来表示，其中$\epsilon$是一个随机变量，即：
\begin{equation}
\tilde{z} \sim g_{\phi}(\epsilon,X), \quad \epsilon \sim p(\epsilon)
\end{equation}
经过这样子的转换后，我们用蒙特卡洛估计某个函数对$Q_{\Phi}(Z|X)$的期望就可以转换成对$p(\epsilon)$求期望：
\begin{align}
E_{Q_{\Phi}(Z|X)}[f(z)]=E_{p(\epsilon)}[f(g_{\phi}(\epsilon,X))]\simeq\frac{1}{L}\sum_{l=1}^{L}f(g_{\phi}(\epsilon^{(l)},X))\quad where \quad \epsilon^{(l)} \sim p(\epsilon)
\end{align}
比如$z\sim Q(Z|X)=\mathcal{N}(\mu, \sigma^2)$，那么一个reparameterization的方法就是让$z=\mu+\sigma*\epsilon，where\ \epsilon\sim \mathcal{N}(0,1)$。用下图来表示reparameterization之前和之后的差别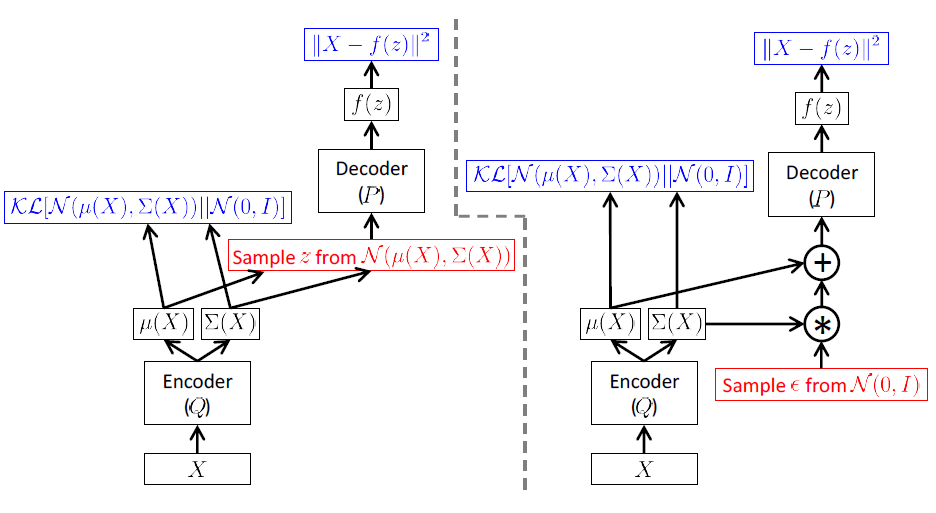

在上图中，使用了$\mathcal{N}(0,1)$作为先验分布，因为理论上，经过足够复杂的变换后，标准正态分布能够映射成相同维度下任意的分布。
$g_{\Phi}$可以根据以下三个条件来选择

所以Auto-Encoding VB的训练算法如下

---

Solution of KL, Gaussian case

下面给出$Q_{\Phi}$和$P(Z)$在高斯情况下的KL熵解析形式，其中$J$是$Z$的维度：
\begin{align}
\int Q_{\Phi}(Z)logP_{\Theta}(Z)dz &= \int \mathcal{N}(Z;\mu, \sigma^2)log\mathcal{N}(Z;0,I)dz \\
&= -\frac{J}{2}log(2\pi)-\frac{1}{2}\sum_{j=1}^{J}(\mu_j^2+\sigma_j^2)
\end{align}
\begin{align}
\int Q_{\Phi}(Z)logQ_{\Phi}(Z)dz &= \int \mathcal{N}(Z;\mu, \sigma^2)log\mathcal{N}(Z;\mu, \sigma^2)dz \\
&= -\frac{J}{2}log(2\pi)-\frac{1}{2}\sum_{j=1}^{J}(1+\sigma_j^2)
\end{align}
所以：
\begin{align}
-D_{KL}(Q_{\Phi}(Z)||P_\Theta(Z)=\frac{1}{2}\sum_{j=1}^{L}(1+log(\sigma_j^2)-\mu_j^2-\sigma_j^2)
\end{align}

---

Marginal likelihood estimator

估计生成模型$p_{\theta}(x,z)=p_{\theta}p_{\theta}(x|z)$的边缘分布$p_{\theta}(x^{(i)})$

---

References

[1]. Tutorial on Variational Autoencoders
[2]. Auto-Encoding Variational Bayes