1. 背景
在概率模型中,我们常常需要得到隐变量的后验分布或者计算相对于某个分布的期望,比如在EM算法中我们需要得到隐变量$Z$的后验分布,以及计算完全数据的似然分布相对于隐变量的后验分布的期望。然而对于很多现实中的模型,常常因为隐变量的维度过高,难以计算;或者期望太过复杂,没有闭式解。这时候我们就要寻求近似解。近似解大体上分为两种,一种是stochastic approximation,如MCMC;另一种是deterministic approximation,比如我们这篇文章要讲的变分推断。
变分法最早来源于微积分,因为涉及到函数空间,所以叫变分。变分法的核心思想,就是从某个函数空间中找到满足某些条件或约束的函数。我们在统计推断中用到的变分法,实际上就是用形式简单的分布,去近似形式复杂、不易计算的分布,这样再做积分运算就会容易的多。
———-
2. 基础推导
跟EM里的推导一样,似然函数可以推导成一个下界加上一个相对熵的形式:
\begin{align}
ln(p(X)) &= ln\left(\frac{p(X,Z)}{q(Z)}\right) - ln\left(\frac{p(Z|X)}{q(Z)}\right) \\
&=\int q(Z)ln\left(\frac{p(X,Z)}{q(Z)}\right)dZ - \int q(Z)ln\left(\frac{p(Z|X)}{q(Z)}\right)dZ \\
&=\underbrace{\int q(Z)ln(p(X,Z))dZ - \int q(Z)ln(q(Z))dZ}_{\mathcal{L}(q)} + \underbrace{\left(-\int q(Z)ln\left(\frac{p(Z|X)}{q(Z)}\right)dZ\right)}_{KL(q||p)} \\
&= \mathcal{L}(q) + KL(q||p)
\end{align}
这里的形式跟EM不同的是参数$\Theta$也包含到了随机变量$Z$里。$\mathcal{L}(q)$叫做Evidence Lower Bound(ELOB),因为相对熵是恒不小于0的。$\mathcal{L}$是关于函数$q(Z)$的泛函【functional】
不同于EM,这里$p(Z|X)$是intractable的,所以在最小化KL divergence的时候,我们需要限制$q(Z)$可选的分布类型——既要tractable,也能提供一个好的approximation。而且,这里不会有”over-fitting”,因为越逼近真实的后验分布越好
———-
3. Mean field
常用的是限制$q(Z)$为可分解的分布【factorized distributions】,将$Z$分解为$M$组变量$Z_i$,即
\begin{equation}
q(Z) = \prod_{i=1}^Mq_i(Z_i)
\end{equation}
这个分解通常与模型相关。在物理上,这种形式的变分推断被称为mean filed theory。
将上式的分解代入到$\mathcal{L}(q)$,为了让表达更加简洁明了,用$q_i$表示$q_i(Z_i)$:
\begin{align}
\mathcal{L}(q) &= \int q(Z)ln(p(X,Z))dZ - \int q(Z)ln(q(Z))dZ \\
&= \underbrace{\int \prod_{i=1}^Mq_iln(p(X,Z))dZ}_{part (1)} - \underbrace{\int \prod_{i=1}^Mq_i\sum_{i=1}^Mlnq_idZ}_{part (2)}
\end{align}
\begin{align}
(Part\ 1) &= \int \prod_{i=1}^Mq_iln(p(X,Z))dZ \\
&= \int_{Z_1}\ldots\int_{Z_M}\prod_{i=1}^Mq_iln(p(X,Z))dZ_1,…,dZ_M \\
&= \int_{Z_j}q_j\left(\int_{Z_{i\neq j}}\prod_{i\neq j}^Mq_iln(p(X,Z))\prod_{i\neq j}^MdZ_i\right)dZ_j \\
&= \int_{Z_j}q_j\left(\int_{Z_{i\neq j}}ln(p(X,Z))\prod_{i\neq j}^Mq_idZ_i\right)dZ_j \\
&= \int_{Z_j}q_j(Z_j)[E_{i\neq j}[ln(p(X,Z))]]dZ_j
\end{align}
\begin{align}
(Part\ 2) &= \int \prod_{i=1}^Mq_i\sum_{i=1}^Mln(q_i)dZ \\
&= \sum_{j=1}^M\left(\int_{Z_j}q_jln(q_j)\left(\int_{Z_{i\neq j}}\prod_{Z_{i\neq j}}q_idZ_{i\neq j}\right)dZ_j\right) \\
&= \sum_{j=1}^M\int_{Z_j}q_jln(q_j)dZ_j
\end{align}
所以,对于某个特定的$q_j$:
\begin{align}
\mathcal{L}(q) &= \int_{Z_j}q_j\underbrace{[E_{i\neq j}[ln(p(X,Z))]]}_{ln(\tilde{p}_j(X,Z_j))}dZ_j - \int_{Z_j}q_jln(q_j)dZ_j + \underbrace{const}_{terms\ not\ involve\ q_j} \\
&= \int_{Z_j}q_jln\frac{ln(\tilde{p}_j(X,Z_j))}{q_j} + const
\end{align}
这也是一个负的KL divergence,所以我们可以通过最小化这个KL divergence来最大化$\mathcal{L}(q)$,这时最优的$q^*_j$满足
\begin{equation}
ln(q_j^*) = E_{i\neq j}[ln(p(X,Z))]
\end{equation}
这条式子的意思是:因子$q_j$最优解的log为完全数据【观测变量和隐变量】的log联合分布相对于其他因子$q_i, i\neq j$的期望——这是变分推断的基础。通常我们不需要考虑const那一项,因为const项就是归一化项,归一化项通常可以通过观察得到。
我们用坐标下降的方法迭代更新每个因子直到收敛。因为下界对于每个因子都是凸的,所以这个过程保证收敛。
———-
4. $KL(p||q)\ vs \ KL(q||p)$
上面用的优化是$KL(q||p)$,现在考虑一般情况下用可分解的$q(Z)$最小化$KL(p||q)$的问题:
\begin{equation}
KL(p||q)=-\int p(Z)\left[\sum_{i=1}^Mln(q_i)\right]dZ+\underbrace{\int p(Z)lnp(Z)dZ}_{const}
\end{equation}
像上面一样只考虑对某个因子$q_j$做优化,则
\begin{align}
KL(p||q) &= -\int p(Z)\left[\sum_{i=1}^Mln(q_i)\right]dZ+const \\
&= -\int\left(p(Z)ln(q_j)+p(Z)\sum_{i\neq j}ln(q_i)\right)dZ + const \\
&= -\int p(Z)ln(q_j)dZ + const \\
&= -\int ln(q_j)\underbrace{\left[\int p(Z)\prod_{i\neq j}dZ_i\right]}_{F_j(Z_j)}dZ_j + const \\
&= -\int F_j(Z_j)ln(q_j)dZ_j + const
\end{align}
用拉格朗日乘子法约束$q_j$为一个分布:
\begin{equation}
-\int F_j(Z_j)ln(q_j)dZ_j + \lambda\left(\int q_jdZ_j -1\right)
\end{equation}
用变分法的欧拉-拉格朗日方程求解可以得到
\begin{equation}
-\frac{F_j(Z_j)}{q_j}+\lambda = 0
\end{equation}
也即
\begin{equation}
\lambda q_j = F_j(Z_j)
\end{equation}
两边对$Z_j$积分,可得
\begin{equation}
\lambda=\int F_j(Z_j)dZ_j=1
\end{equation}
所以
\begin{equation}
q_j = F_j(Z_j) = \int p(Z)\prod_{i\neq j}dZ_i = p(Z_j)
\end{equation}
就是说,在优化$KL(p||q)$的情况下,因子$q_j$的最优解有刚好就是相应的边缘分布$p(Z_j)$
PRML里的一幅图描述了对二元高斯分布分别用$KL(q||p)$和$KL(p||q)$优化的结果
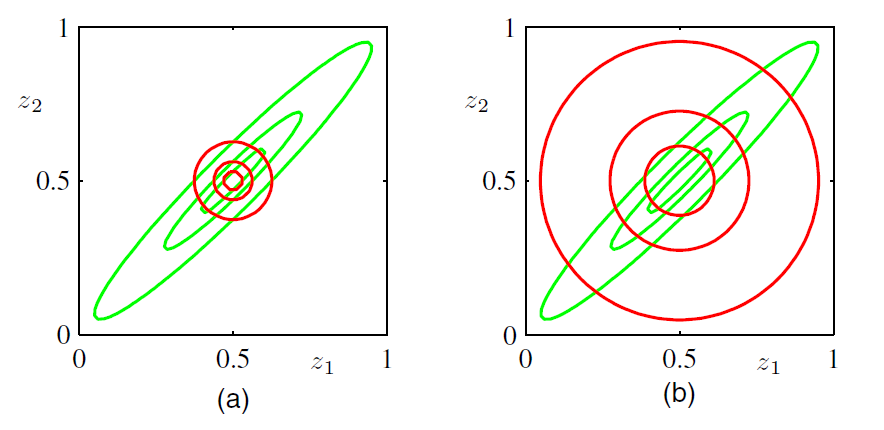
左边是$KL(q||p)$,右边是$KL(p||q)$,两种情况下都能很好得拟合均值,然而对于整体分布的拟合情况确有很大差别。这可以从KL divergence的式子里直接考虑
\begin{equation}
KL(q||p)=-\int q(Z)ln\frac{p(Z)}{q(Z)}dZ
\end{equation}
这里对值影响比较大的部分主要来自$ln$相除的那部分。对于$KL(q||p)$,在$p(Z)$比较小的地方$q(Z)$也得比较小,不然的话一除,再ln,这个值就会非常大,这叫”zero forcing”;相反,对于$KL(p||q)$的情况,在$p(Z)$比较大的地方,$q(Z)$也得比较大,这种情况叫”zero avoiding”。这就造成了上图左边只在高密度区域有值,而右边则是整体上都有值的结果。
———-