在机器学习的领域里面，我们常常需要用极大似然估计【或极大化后验】的方法去做参数估计
\begin{equation}
\theta^{MLE}=argmax_{\theta}(\mathcal{L}(\theta))=argmax_{\theta}(ln[p(X|\theta)])
\end{equation}
然而，当模型中含有隐变量，或者说观测数据不完整时，用极大似然估计往往不能得到一个闭式解【closed-form solution】。EM算法就是一种求解这种含有隐变量模型的迭代算法。

我们用$Z$表示所有的隐变量，$X$表示所有的观察到的变量，$\Theta$表示所有的参数，则log likelihood可以写成：
\begin{align}
\mathcal{L}(\Theta|X) & = ln(p(X|\Theta))\\
&= ln\left(\frac{p(X,Z|\Theta)}{p(Z|X,\Theta)}\right) \\
&= ln\left(\frac{p(X,Z|\Theta)}{Q(Z)}*\frac{Q(Z)}{p(Z|X,\Theta)}\right)\\
&= ln\left(\frac{p(X,Z|\Theta)}{Q(Z)}\right)+ln\left(\frac{Q(Z)}{p(Z|X,\Theta)}\right)
\end{align}
两边对Q(Z)这个分布求期望，左边因为不含变量$Z$，所以不会影响：
\begin{align}
ln(p(X|\Theta)) &= \int_ZQ(Z)ln\left(\frac{p(X,Z|\Theta)}{Q(Z)}\right)+\int_ZQ(Z)ln\left(\frac{Q(Z)}{p(Z|X,\Theta)}\right) \\
&= \int_ZQ(Z)ln\left(\frac{p(X,Z|\Theta)}{Q(Z)}\right)+\underbrace{KL(Q(Z)||p(Z|X,\Theta))}_{\ge0} \\
&= \mathcal{L}(\Theta,Q) + KL(Q(Z)||p(Z|X,\Theta)) \\
&\ge \mathcal{L}(\Theta,Q)
\end{align}
也即$L(\Theta,Q)$是$ln(p(X|\Theta))$的下界。引用PRML里的一幅图来形象说明它们之间的关系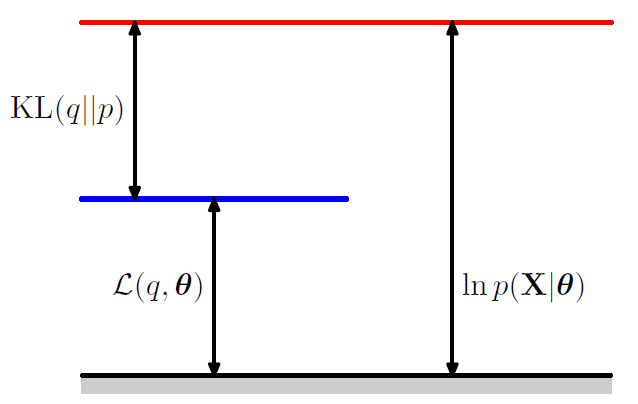

所以EM其实是一个Maximize-Maximize的过程【$\Theta^{old}$表示上一次迭代$\Theta$的值】：

在E步，我们固定住$\Theta^{old}$，优化下界【with respect to $Q(Z)$】，这时候下界最大当且仅当KL divergence为0，也即$Q(Z)=p(Z|X,\Theta^{old})$；

在M步，我们固定住$Q(Z)$，优化下界【with respect to $\Theta$】，得到$\Theta^{new}$

这样子，每一步优化下界都在改进，所以EM一定会收敛，但是EM并不保证收敛到最优解
另一种证明$ln(p(X|\Theta))\ge F(\Theta, Z)$的方法是利用琴生不等式【Jensen’s Inequality】：
\begin{align}
ln(p(X|\Theta) &= ln\int_Zp(X,Z|\Theta) \\
&= \underbrace{ln\left(\int_Z\frac{p(X,Z|\Theta)}{Q(Z)}Q(Z)\right)}_{lnE_{Q(Z)}[f(Z)]} \\
&\ge \underbrace{\int_Zln\left(\frac{p(X,Z|\Theta)}{Q(Z)}\right)Q(Z)}_{E_{Q(Z)}ln[f(Z)]}
\end{align}
接下来再讲一下M步里怎么优化下界，做完E步后KL divergence那一项变成0，即$Q(Z)=p(Z|X,\Theta^{old})$，所以
\begin{align}
\mathcal{L}(\Theta|X) &= \mathcal{L}(\Theta, Q) \\
&= \int_ZQ(Z)ln\left(\frac{p(X,Z|\Theta)}{Q(Z)}\right) \\
&= \underbrace{\int_Zp(Z,X| \Theta^{old})ln(p(X,Z|\Theta))}_{Q(\Theta, \Theta^{old})}-\underbrace{\int_Zp(Z|X, \Theta^{old})ln(p(Z|X, \Theta^{old}))}_{independent\ of\ \Theta}
\end{align}
也就是我们只需要最大化$Q(\Theta, \Theta^{old})$
注意到现在我们要优化的参数$\Theta$只存在于log里面，如果分布$p(X,Z|\Theta)$是一个指数族分布，那么log和exp将会抵消，我们求解起来就会比原来直接求$p(X|\Theta)$简单得多
类似地，EM也可以用来做极大后验估计：
\begin{align}
ln(p(\Theta|X) &= ln(p(\Theta,X))-ln(p(X)) \\
&= ln(p(X|\Theta)) + ln(p(\Theta)) - ln(p(X))
\end{align}
对$ln(p(X|\Theta))$做和上面一样的分解即可

“Tagare” approach

另一种证明EM会收敛的方法，大同小异
\begin{align}
\mathcal{L}(\Theta|X) &= ln(p(X|\Theta)) \\
&= ln\left(\frac{p(X,Z|\Theta)}{p(Z|X,\Theta)}\right) \\
\end{align}
\begin{align}
&\Rightarrow \int_zln(p(X|\Theta))p(Z|X, \Theta^{old}) \\
&= \int_Zln(p(Z,X|\Theta))p(Z|X, \Theta^{old})dZ-\int_Zln(p(Z|X,\Theta))p(Z|X, \Theta^{old})dZ
\end{align}
\begin{align}
&\Rightarrow ln(p(X|\Theta))\\
&= \underbrace{\int_Zp(Z,X| \Theta^{old})ln(p(X,Z|\Theta))}_{Q(\Theta, \Theta^{old})}-\underbrace{\int_Zp(Z|X, \Theta^{old})ln(p(Z|X, \Theta))}_{H(\Theta, \Theta^{old})}
\end{align}
我们只maximize $Q(\Theta, \Theta^{old})$，因为可以证明
\begin{equation}
argmax_{\Theta}Q(\Theta, \Theta^{old})=\Theta^{new} \Rightarrow H(\Theta^{new}, \Theta^{old}) \le H(\Theta^{old}, \Theta^{old})
\end{equation}
这样子，我们就有
\begin{equation}
\mathcal{L}(\Theta^{new})=Q(\Theta^{new}, \Theta^{old})-H(\Theta^{new}, \Theta^{old}) \ge Q(\Theta^{old}, \Theta^{old})-H(\Theta^{old}, \Theta^{old}) = \mathcal{L}(\Theta^{old})
\end{equation}
可以用琴生不等式证明$H(\Theta^{old}, \Theta^{old})-H(\Theta, \Theta^{old}) \ge 0\quad \forall\Theta$